|Définitions, exemples| |Construction, programmes| |Graphes et hypergraphes| |Pavages infinis ou mixtes ou circulaires|

Pavages rythmiques parfaits IV
Quintuplets ou plus
De n=2 jusqu'à n=27, il n'y a pas de pavage rythmique parfait par des quintuplets.
Quelques essais, utilisant cette fois des algorithmes de recherche de cliques (voir plus loin), n'ont pas permis pour l'instant d'obtenir de pavages rythmiques parfaits d'ordres 5 ou plus.
Voici un exemple où l'on a réussi à placer 29 progressions arithmétiques au lieu des 32 espérées (n=32, k=5) :
Quelques essais, utilisant cette fois des algorithmes de recherche de cliques (voir plus loin), n'ont pas permis pour l'instant d'obtenir de pavages rythmiques parfaits d'ordres 5 ou plus.
Voici un exemple où l'on a réussi à placer 29 progressions arithmétiques au lieu des 32 espérées (n=32, k=5) :
3 10 7 0 4 12 6 9 1 6 0 3 6 10 1 6 11 0 6 8 1 21 3 * 0 10 1 24 19 18 * 0 1 3 7 26 13 10 16 12 15 4 9 16 3 21 11 * 16 10 26 19 8 16 17 24 * 27 16 * 18 * 13 * 14 26 7 15 17 21 * 23 20 12 19 22 11 9 4 27 26 20 17 24 14 8 * 23 13 * 20 18 22 21 15 26 17 19 7 20 * 27 * 23 14 * 11 12 20 22 17 24 9 * 13 4 * 21 8 23 19 15 18 27 14 25 22 25 * 25 7 25 * 25 * 23 11 * 5 24 13 12 5 22 14 27 5 9 15 * 5 8 4 18 5 2 2 2 2 2

Pavages par des suites de longueurs quelconques
On peut trouver des pavages par des suites arithmétiques de raisons différentes, n'ayant pas toutes la même longueur.
Le pavage ci-dessous est constitué d'une suite arithmétique de sept termes, d'une autre de cinq termes et enfin de six suites de trois termes. Les raisons de ces suites sont toutes différentes et supérieures ou égales à 3.
Ce pavage a permis de composer le morceau de musique suivant. À chaque nombre est associé un motif musical, les apparitions de ces motifs sont réglées par le pavage.
Le second exemple est plus long et les suites arithmétiques ont une longueur supérieure ou égale à 4 :
0 1 2 3 0 4 3 5 0 3 6 1 0 5 4 2 0 7 6 5 0 1 7 4 0 5 6 7 2
Ce pavage a permis de composer le morceau de musique suivant. À chaque nombre est associé un motif musical, les apparitions de ces motifs sont réglées par le pavage.
Le second exemple est plus long et les suites arithmétiques ont une longueur supérieure ou égale à 4 :
0 1 0 2 0 3 0 4 0 5 0 6 0 5 7 4 3 5 8 1 9 5 2 4 7 5 10 3 6 10 11 4 10 8 7 10 9 1 3 4 12 2 11 13 7 6 14 15 8 12 13 14 9 15 11 1 14 13 12 15 2 14 6 8 13 15 11 12 9
Pavages rythmiques parfaits infinis
Existence
Il existe des pavages rythmiques parfaits infinis de tout ordre k supérieur ou égal à 2, il suffit d'appliquer un algorithme glouton pour les construire :
Au départ U et R sont deux ensembles vides.
a) chercher le plus petit naturel 'a' qui n'est pas dans U.
b) choisir la plus petite raison 'r' supérieure ou égale à 1 qui ne soit pas dans R et utilisable, c'est-à-dire telle que a, a+r, ..., a+(k-1)*r ne soient pas dans U (pas déjà utilisés).
Ajouter a, a+r, ..., a+(k-1)*r dans U et r dans R.
C'est possible car a+r-1 est au plus égal au plus grand élément de U (le plus grand naturel utilisé dans les précédentes progressions).
reprendre a) et b) indéfiniment.
Au départ U et R sont deux ensembles vides.
a) chercher le plus petit naturel 'a' qui n'est pas dans U.
b) choisir la plus petite raison 'r' supérieure ou égale à 1 qui ne soit pas dans R et utilisable, c'est-à-dire telle que a, a+r, ..., a+(k-1)*r ne soient pas dans U (pas déjà utilisés).
Ajouter a, a+r, ..., a+(k-1)*r dans U et r dans R.
C'est possible car a+r-1 est au plus égal au plus grand élément de U (le plus grand naturel utilisé dans les précédentes progressions).
reprendre a) et b) indéfiniment.
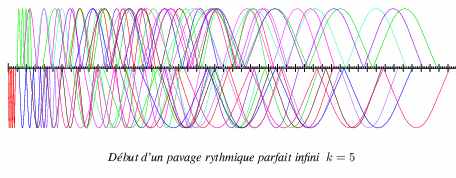
On peut aussi construire de la même façon des pavages rythmiques mixtes infinis en faisant varier les longueurs des progressions arithmétiques.
Il est facile de voir que l'ensemble des pavages rythmiques mixtes infinis contient les ensembles de pavages rythmiques parfaits infinis d'ordre k supérieurs ou égaux à 2 quelconques.
Les pavages rythmiques parfaits finis d'ordre k sont tous contenus dans des pavages rythmiques parfaits infinis.
Il est facile de voir que l'ensemble des pavages rythmiques mixtes infinis contient les ensembles de pavages rythmiques parfaits infinis d'ordre k supérieurs ou égaux à 2 quelconques.
Les pavages rythmiques parfaits finis d'ordre k sont tous contenus dans des pavages rythmiques parfaits infinis.