Accueil / Pavages rythmiques parfaits
Suites de Skolem
Seminaire_Maths_Musique
ANNONCE : ouverture candidatures Master / ingénieur
a
2013
Objet : [gdr-im] Offre de stage, algorithmique du texte et formes sonates (Lille)
... lire la totalité de ce message
|Définitions, exemples| |Construction, programmes| |Graphes et hypergraphes| |Pavages infinis ou mixtes ou circulaires|

Pavages rythmiques parfaits I
Les lecteurs de l'article de Jean-Paul Delahaye N° 325 novembre 2004 de la revue Pour la Science et aussi de l'article N° 329 mars 2005, « La délicate géométrie du carré », trouveront ici des compléments sur les pavages rythmiques parfaits.
Les suites finies de nombres que vous pouvez voir dans ces pages sont des généralisations de celles du norvégien Thoralf Skolem (construites en 1957 pour obtenir des systèmes triples cycliques de Steiner) et de celles de l'écossais Dudley Langford à la même époque (des puzzles).
À la page d'introduction, vous pourrez voir et construire des suites de Skolem (à l'aide de paires), des systèmes de Skolem, des systèmes de différences et des systèmes triples de Steiner d'ordre 6n+1.
De nombreuses inconnues subsistent, ainsi personne n'a été capable de construire des séquences à partir de quintuplets ou plus, ni même de montrer leur existence ou de la réfuter. Le tableau de la page suivante montre qu'il n'en existe pas pour k=5 et n<28 (recherches personnelles par ordinateur).
.
Les suites finies de nombres que vous pouvez voir dans ces pages sont des généralisations de celles du norvégien Thoralf Skolem (construites en 1957 pour obtenir des systèmes triples cycliques de Steiner) et de celles de l'écossais Dudley Langford à la même époque (des puzzles).
À la page d'introduction, vous pourrez voir et construire des suites de Skolem (à l'aide de paires), des systèmes de Skolem, des systèmes de différences et des systèmes triples de Steiner d'ordre 6n+1.
De nombreuses inconnues subsistent, ainsi personne n'a été capable de construire des séquences à partir de quintuplets ou plus, ni même de montrer leur existence ou de la réfuter. Le tableau de la page suivante montre qu'il n'en existe pas pour k=5 et n<28 (recherches personnelles par ordinateur).
.
Premier exemple de pavage rythmique parfait
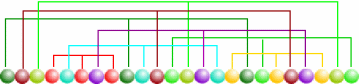
Les 24 billes de l'image ci-dessus sont de 8 couleurs différentes.
Définition
Un pavage rythmique parfait d'ordre k et de dimension n est
une suite finie de k*n termes entiers telle que
 chaque entier de 0 à n-1 inclus est égal à exactement k termes de la suite,
chaque entier de 0 à n-1 inclus est égal à exactement k termes de la suite,
 les rangs de ces k termes égaux forment une progression arithmétique
les rangs de ces k termes égaux forment une progression arithmétique
 les raisons de ces progressions sont toutes différentes.
les raisons de ces progressions sont toutes différentes.
On peut aussi le définir comme une partition des premiers k*n naturels en n parties de k éléments régulièrement espacés, de raisons ou espacements tous différents.
On peut aussi le définir comme une partition des premiers k*n naturels en n parties de k éléments régulièrement espacés, de raisons ou espacements tous différents.
Notations
Suite d'entiers
L'image ci-dessus représente un pavage rythmique parfait d'ordre 3 et de dimension 8 que l'on peut écrire :
qui est une suite finie de
On pourrait sans inconvénient utiliser les lettres de l'alphabet pour écrire le même pavage :
(0, 1, 2, 3, 4, 3, 5, 3, 0, 4, 1, 6, 2, 5, 4, 7, 0, 6, 7, 1, 5, 7, 2, 6)
qui est une suite finie de
3*8 = 24 entiers compris entre 0 et 7 (mis à la place des huit couleurs de la figure).
On pourrait sans inconvénient utiliser les lettres de l'alphabet pour écrire le même pavage :
A B C D E D F D A E B G C F E H A G H B F H C G
Partition
En relevant les positions dans le pavage d'un même terme on obtient une partition de {0, 1, ..., 23} par les huit sous-ensembles :
Rangés dans l'ordre croissant, les éléments de chaque ensemble forment une suite arithmétique (voir ci-dessous).
{0, 8, 16}, {1, 10, 19}, {2, 12, 22}, {3, 5, 7}, {4, 9, 14}, {6, 13, 20}, {11, 17, 23}, {15, 18, 21}
Rangés dans l'ordre croissant, les éléments de chaque ensemble forment une suite arithmétique (voir ci-dessous).
Suites arithmétiques
On pourrait donc aussi bien écrire les les progressions arithmétiques suivantes :
La première progression
On vérifie que la suite croissante 3, 5, 7 est une progression arithmétique de trois termes en calculant les différences 5-3 et 7-5, toutes deux égales à la valeur 2 qui est la raison de cette progression.
Les raisons des huit progressions sont, dans l'ordre, 8, 9, 10, 2, 5, 7, 6, 3, elles sont toutes différentes. Il suffit de connaître ces huit nombres, dans l'ordre, (et la longueur des progressions) pour reconstituer le pavage.
(0, 8, 16), (1, 10, 19), (2, 12, 22), (3, 5, 7), (4, 9, 14), (6, 13, 20), (11, 17, 23), (15, 18, 21)
La première progression
(0, 8, 16)
donne les trois positions du nombre 0 (ou de la lettre A) dans le pavage. De même (3, 5, 7) donne les positions du nombre 3 (ou de la lettre D).
On vérifie que la suite croissante 3, 5, 7 est une progression arithmétique de trois termes en calculant les différences 5-3 et 7-5, toutes deux égales à la valeur 2 qui est la raison de cette progression.
Les raisons des huit progressions sont, dans l'ordre, 8, 9, 10, 2, 5, 7, 6, 3, elles sont toutes différentes. Il suffit de connaître ces huit nombres, dans l'ordre, (et la longueur des progressions) pour reconstituer le pavage.
Exemples
Couples
Lorsque k=2, la suite A060963 de N.J.A. Sloane donne les nombre de partitions des 2n premiers naturels, c.-à-d. des p. r. p. d'ordre 2 jusqu'à n=6.
On peut prolonger cette suite en calculant les termes jusqu'au rang n=13 :
1, 1, 5, 29, 145, 957, 8397, 85169, 944221, 11639417, 160699437, 2430145085, 39776366397
(les 39776366397 pavages de rang 13 ont effectivement été construits par le programme, ce qui a pris un certain temps !)
On peut bien évidemment construire des pavages de dimensions n bien plus élevées. Le petit morceau de musique ci-dessous correspond à n=508. Chacune de ses 508 combinaisons de 3 notes (trois voix) est joué deux fois à des intervalles de temps tous différents.
On peut prolonger cette suite en calculant les termes jusqu'au rang n=13 :
1, 1, 5, 29, 145, 957, 8397, 85169, 944221, 11639417, 160699437, 2430145085, 39776366397
(les 39776366397 pavages de rang 13 ont effectivement été construits par le programme, ce qui a pris un certain temps !)
On peut bien évidemment construire des pavages de dimensions n bien plus élevées. Le petit morceau de musique ci-dessous correspond à n=508. Chacune de ses 508 combinaisons de 3 notes (trois voix) est joué deux fois à des intervalles de temps tous différents.
Triplets
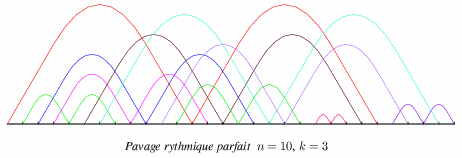
Ce pavage de 10 triplets est
0 1 2 3 1 4 5 1 3 2 6 7 0 3 4 7 2 5 6 7 8 8 8 4 0 9 6 9 5 9
Quadruplets

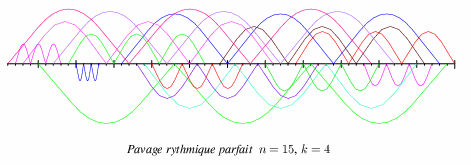
Pavage rythmique parfait d'ordre 4
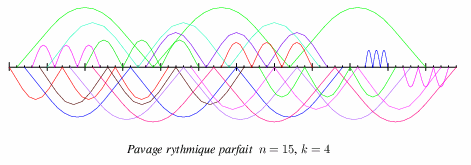
Les deux seuls pavages rythmiques parfaits de 60 points sont le pavage
représenté sur l'image ci-dessus et le pavage symétrique
0 1 2 3 4 5 3 0 6 3 7 8 3 4 0 7 2 5 9 1 7 0 4 6 10 7 9 8 11 5 2 4 11 12 9 10 11 1 6 12 11 5 9 8 2 12 10 13 13 13 13 12 14 6 14 1 14 10 14 8
représenté sur l'image ci-dessus et le pavage symétrique
0 1 2 1 3 1 4 1 5 6 6 6 6 2 5 7 0 8 9 10 5 4 3 10 2 8 5 10 11 7 9 10 0 8 12 2 4 11 13 12 3 8 9 7 12 13 11 14 0 12 14 4 13 14 9 11 14 7 3 13
Un pavage de 27x4 = 108 points est donné ci-dessous
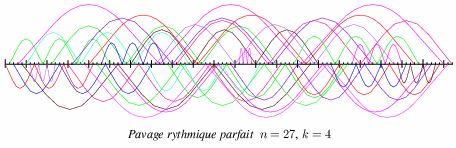
Ce pavage est
Un autre mode de représentation des pavages rythmiques utilise des segments de droites et permet d'illustrer la définition par les propriétés géométriques de la figure obtenue.
Le pavage (n=23, k=4)
est représenté par la figure
0 1 2 3 4 5 6 0 6 1 6 7 6 2 0 8 9 1 5 10 11 0 12 13 2 1 14 4 13 7 15 5 8 13 16 2 17 3 13 18 9 19 12 16 5 15 11 7 10 8 4 14 16 18 20 17 21 21 21 21 15 16 12 19 9 7 8 18 22 23 20 3 11 4 17 15 14 10 24 23 22 18 12 25 24 19
20 25 9 23 24 25 22 17 26 25 24 26 11 23 26 14 20 26 22 3 10 19
Un autre mode de représentation des pavages rythmiques utilise des segments de droites et permet d'illustrer la définition par les propriétés géométriques de la figure obtenue.
Le pavage (n=23, k=4)
0 1 2 3 4 5 6 7 2 8 9 10 11 3 2 0 12 13 14 12 2 5 12 3 9 12 8 15 1 4 0 11 6 3
10 7 16 5 9 13 16 17 14 8 16 0 17 15 16 18 11 17 9 5 4 1 17 10 6 19 8 13 18 7 20 21 14 15 19 11 22 20 22 21 22 18 22 19 20 4 10 21 1 13 6 20 19 15 18 21 14 7
est représenté par la figure
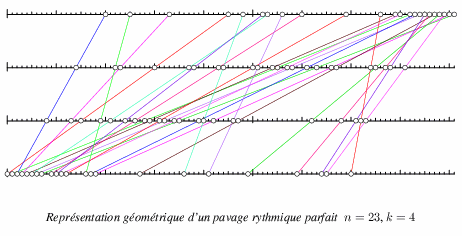
Sur cette figure, les quatre lignes horizontales coupent les vingt-trois segments en quatre points (deux extrémités et deux points intermédiaires). Les abscisses des quatre points d'intersections donnent les quadruplets d'un pavage rythmique parfait d'ordre 4.
On vérifie assez facilement que :
 Les quadruplets sont en progression arithmétique car les quatre droites horizontales sont régulièrement espacées.
Les quadruplets sont en progression arithmétique car les quatre droites horizontales sont régulièrement espacées.
 Les raisons des progressions arithmétiques sont toutes diffférentes car les orientations sont toutes distinctes.
Les raisons des progressions arithmétiques sont toutes diffférentes car les orientations sont toutes distinctes.
 Tous les naturels plus petits que k*n = 4*24 se trouvent dans une progression unique, on peut en effet vérifier sur la figure que deux points d'intersection ne sont jamais à la verticale l'un de l'autre.
Tous les naturels plus petits que k*n = 4*24 se trouvent dans une progression unique, on peut en effet vérifier sur la figure que deux points d'intersection ne sont jamais à la verticale l'un de l'autre.
Un pavage rythmique parfait de taille 40x4 :

(Les 40 progressions sont numérotées de 0 à 39).
On vérifie assez facilement que :
Un pavage rythmique parfait de taille 40x4 :

0 1 2 3 4 5 5 5 5 6 7 8 9 7 10 11 7 12 13 7 14 15 16 17 18 3 16 8 19 20 16 21 6 22 16 23 17 24 9 2 25 20 0 8 1 26 11 3 18 17 14 4 13 20 24 6 21 15 10 8 19 22 17 12 9 20 27 28 29 3 23 24 18 30 26 28 2 11 6 25 14 21 31 28 0 27 13 1 24 22 9 28 19 15 30 29 18 31 4 32 33 34 10 26 27 23 21 35 11 12 14 34 31 2 33 30 35 22 25 32 13 34 29 27 19 35 0 31 33 15 1 34 26 36 35 37 30 38 36 32 23 37 33 36 38 4 10 37 36 29 39 38 39 37 39 12 39 25 38 32
(Les 40 progressions sont numérotées de 0 à 39).
Quintuplets ou plus
De n=2 jusqu'à n=27, il n'y a pas de pavage rythmique parfait par des quintuplets.
Quelques essais, utilisant diverses méthodes et en particulier des algorithmes de recherche de cliques (voir plus loin), n'ont pas permis pour l'instant d'obtenir de pavages rythmiques parfaits d'ordres 5 ou plus.
Quelques essais, utilisant diverses méthodes et en particulier des algorithmes de recherche de cliques (voir plus loin), n'ont pas permis pour l'instant d'obtenir de pavages rythmiques parfaits d'ordres 5 ou plus.
Liens

|Définitions, exemples| |Construction, programmes| |Graphes et hypergraphes| |Pavages infinis ou mixtes ou circulaires|
Pour un premier contact, [utilisez ce formulaire] ou utilisez l'adresse de messagerie qui y figure. Merci d'indiquer la page précise du site "http//jm.davalan.org/...", cela m'aidera beaucoup. Ne joignez aucun document à votre message.
Jeux-et-Mathématiques n'est pas un site commercial. Aucun des liens placés sur ce site n'est rémunéré, ni non plus aucune des informations données.
Important : Si votre question a un quelconque rapport avec un travail personnel (Devoir TIPE Master...) , vous devez absolument me le préciser dès votre premier message et m'indiquer très précisément les limites des informations demandées. Vous devez aussi avertir la personne qui dirige éventuellement votre travail ou le corrige de cette communication et lui montrer les documents fournis.
© (Copyright) Jean-Paul Davalan 2002-2014Important : Si votre question a un quelconque rapport avec un travail personnel (Devoir TIPE Master...) , vous devez absolument me le préciser dès votre premier message et m'indiquer très précisément les limites des informations demandées. Vous devez aussi avertir la personne qui dirige éventuellement votre travail ou le corrige de cette communication et lui montrer les documents fournis.
J'essaie de répondre aux questions posées, mais ne lis pas les documents mathématiques amateurs, pas plus que je ne donne mon avis sur les démonstrations des conjectures de Collatz ou autres. Je ne lis pas les documents word, je ne corrige pas les programmes informatiques et depuis des années je n'utilise plus de tableur.
![]()