Accueil
Plan du site
Bloc notes
Jeux
Graphes
Combinatoire
Arithmétique
Algèbre
Analyse
Probabilités
Automates
Programmation
Divers
Liens
Home
Plan du site
Bloc notes
Jeux
Graphes
Combinatoire
Arithmétique
Algèbre
Analyse
Probabilités
Automates
Programmation
Divers
Liens
Home
Suite de Fibonacci (+ suite de Lucas) - Fibonacci numbers
| SOMMAIRE | Pages Web | Associations | Pages Personnelles | Algorithmes | Problèmes | Demos |
| Exemples | Java | Sujets | Papiers | Journaux | Cours | Tutoriels | Historiques |
| Biographies | Arts | Jeux | Archives | Liens |
| Exemples | Java | Sujets | Papiers | Journaux | Cours | Tutoriels | Historiques |
| Biographies | Arts | Jeux | Archives | Liens |
Calcul de la suite de Fibonacci
PAGES WEB
En particulier le morphisme 0 -> 1, 1 -> 10, quadrillage, billard carré, bracelets... Nombres de Pisano. Générateur de formules. Nombreux calculs en javascript ou applets en java.
<http://perso.wanadoo.fr/jean-paul.davalan/divers/fibonacci/index.html>
Semaine des mathématiques 21-25 novembre 2005
Sous cette même question générique, la CEM propose aux maîtres de tous les ordres d?enseignement, du primaire à l'enseignement supérieur (UNI+HES) de faire travailler leurs élèves sur un même thème : explorer des suites de nombres et leurs propriétés.
Pourquoi ?
* promouvoir la cohérence de l'enseignement des mathématiques durant toute la scolarité, du primaire à l'Université
* conjuguer avec tous les élèves travail sur le sens et la compréhension et acquisition de savoirs mathématiques
* ouvrir les mathématiques et leur enseignement sur la cité
<http://php.educanet2.ch/math/semainedesmaths2005/act_liens.html>
Maîtrise MASS "technologies de la connaissance" le cours
<http://brassens.upmf-grenoble.fr/IMSS/mamass/graphecomp/Fibon/Fibon.html>
This is the Home page for the Fibonacci numbers, the Golden section and the Golden string.
<http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fib.html>
<http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fibpi.html>
<http://www.ee.surrey.ac.uk/Personal/R.Knott/Fibonacci/fibrab.html>
nombre d'or Matila Ghyka
<http://membres.lycos.fr/morvillier/hist.htm>
Thoki Yenn
Square to Silver Rectangle, Square to Bronze Rectangle, Silver Rectangle to Golden Rectangle
<http://www.thok.dk/geometry.html>
Uwe Grimm
<http://mcs.open.ac.uk/ugg2/quasi.html-ssi>
Marc Renault
<http://www.math.temple.edu/~renault/fibonacci/fib.html>
TPE. Laure & Gaëlle Ãlèves de 1ère S, Lycée Charles Baudelaire, Annecy
<http://site.voila.fr/nombredor>
MATsch Université Libre de Bruxelles
[Au bridge] Il s'agit de dénombrer les séquences d'enchères disponibles entre deux paliers donnés, en supposant que le partenaire utilise à chaque tour l'enchère la plus économique disponible (principe du relais).
<http://www.ulb.ac.be/soco/matsch/recherche/32/bridge/barsalou.htm>
by R.Knott, D.A.Quinney and PASS Maths (+plus magazine issue 3 september 1997)
<http://plus.maths.org/issue3/fibonacci/index.html>
JP Chabert
<http://jpm-chabert.club.fr/indexbis.htm>
<http://home.comcast.net/~lkrakauer/weight.htm>
Michael Becker
<http://www.ijon.de/mathe/fibonacci/index.html>
ASSOCIATIONS
PAGES PERSONNELLES - HOME PAGES
Aperiodic Order: People and Research Groups
Michael Baake and Uwe Grimm
<http://mcs.open.ac.uk/ugg2/quasi/people.html-ssi>
ALGORITHMES
Museum of Harmony Fibonacci Computers
<http://www.goldenmuseum.com/1202FibCdeTransf_engl.html>
PROBLÈMES - PROBLEMS
<http://www.primepuzzles.net/problems/prob_031.htm>
DEMOS
Linéaires : Fibonacci, Lucas, Perrin, Padovan. Suites de Somos.
<http://perso.wanadoo.fr/jean-paul.davalan/mots/suites/index.html>
EXEMPLES - EXAMPLES
Dan Litchfield and Dave Goldenheim with support from Charles H. Dietrich
Divide any line segment into a regular partition of any number of parts.
<http://www.scientium.com/diagon_alley/archival/segments/euclid1.htm>
JAVA
Steffen Weber
In the Crystallography of Quasicrystals a quasiperiodic structure is described in terms of a higher-dimensional (nD) periodic crystal. Suitable projections from the latter then yield the quasiperiodic arrangement. A textbook example for an analogon in one-dimensional space (1D) is the Fibonacci chain, which consists of two segments of different lengths (L-long and S-short). Their ratio L/S is tau=(SQRT(5)+1)/2=1.61803...
This applet demonstrates the projection algorithm. The solid line represents the 1D arrangement which is obtained from the the higher-dimensional space (2D periodic square lattice) under the given slope. If the slope is irrational eg.: 31.7..degree (corresponds to ARCTAN(1/tau) [rad]) a quasiperiodic sequence like the Fibonacci chain is obtained. For a rational slope the arrangement will be periodic, whereby the period may be large if the slope is close to an irrational one. In Quasicrystallography such arrangements are called approximants.
<http://jcrystal.com/steffenweber/JAVA/jfibo/jfibo.html>
SUJETS - SUBJECTS
Brancaz Emmanuelle
<http://perso.univ-rennes1.fr/vincent.langlois/Enseignement/L3-SVE/brancaz.doc>
DOCUMENTS - PAPERS
Richard S. Smith, Soazig Guyomarc'h, Therese Mandel, Didier Reinhardt, Cris Kuhlemeier, Przemyslaw Prusinkiewicz: A plausible model of phyllotaxis. Proceedings of the National Academy of Sciences 103 (5), pp. 1301-1306.
A striking phenomenon unique to the kingdom of plants is the regular arrangement of lateral organs around a central axis, known as phyllotaxis... we created a computer simulation model based on data described previously or in this paper and reasonable hypotheses...
<http://algorithmicbotany.org/papers/phyllo.pnas2006.html>
JOURNAUX - LETTERS
<http://www.sdstate.edu/~wcsc/http/fibhome.html>
COURS - COURSES
Document Word (Length: 2,966,528)
<http://www.lacim.uqam.ca/~plouffe/tms/>
TUTORIELS - TUTORIALS - TUTORS
Jacques Binet est né le 2 février 1786 à Rennes, France, et mourut à Paris le 12 mai 1856. Entré à l'Ãcole polytechnique de Paris le 22 novembre 1804, il en gradua en 1806. Par la suite, il travailla au Département des Ponts et Chaussées pour le gouvernement français. En 1807, il devint professeur à l'Ãcole polytechnique; il a aussi détenu la chaire d'astronomie au Collège de France en 1823.
<http://www.virtuel.collegebdeb.qc.ca/maths/dep/binet.htm>
HISTORIQUES - HISTORY
à vérifier ! (équation du 3e degré par exemple).
<http://worldserver2.oleane.com/fatrazie/fibonacci.html>
In 1753 Simson noted that, as the Fibonacci numbers increased in magnitude, the ratio between adjacent numbers approached the golden ratio, whose value is (1 +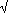 
5)/2 = 1.6180 . . . .
<http://www-history.mcs.st-andrews.ac.uk/history/Mathematicians/Simson.html>
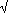5)/2 = 1.6180 . . . . né à Pise 1170, probalement décédé en Italie en 1250.
<http://www.bib.ulb.ac.be/coursmath/bio/fibonacc.htm>
4 April 1842 - 3 Oct 1891
School of Mathematics and Statistics University of St Andrews, Scotland
<http://www-groups.dcs.st-and.ac.uk/~history/Mathematicians/Lucas.html>
Richard Padovan
Born in 1935, Richard Padovan studied architecture at the Architectural Association, London (1952-57). Since then he has combined practice with teaching and writing on architecture. He believes, however, that his real architectural education began when in encountered the work and thought of the Dutch Benedictine architect Dom Hans van der Laan in 1974.
<http://www.nexusjournal.com/N2002-Padovan.html>
BIOGRAPHIES
A brief biographical sketch of Fibonacci, his life and and times and his mathematical achievements.
<http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fibBio.html>
ARTS
Alexey Stakhov, Anna Sluchenkova
<http://www.goldenmuseum.zibys.com/>
JEUX - GAMES
Chaque joueur peut retirer jusqu'au double des pions enlevés par son adversaire au tour précédent.
J-P. Davalan
<http://nim.site.voila.fr/fib/index.html>
ARCHIVES
The Sequence of Fibonacci and the Palazzo della Signoria in Florence
Maria Teresa Bartoli, "The Sequence of Fibonacci and the Palazzo della Signoria in Florence", pp. 31-42 in Nexus V: Architecture and Mathematics, ed. Kim Williams and Francisco Delgado Cepeda, Fucecchio (Florence): Kim Williams Books, 2004.
Maria Teresa Bartoli examined the Fibonacci Sequence and its use in the architectural design of the Palazzo della Signoria in Florence, at the Nexus 2004 conference.
<http://www.nexusjournal.com/conferences/N2004-Bartoli.html>
LIENS - LINKS
Further sources of Information on Fibonacci Numbers and the Golden Section
<http://www.ee.surrey.ac.uk/Personal/R.Knott/Fibonacci/fibrefs.html>
MathSoft
<http://www.mathsoft.com/mathresources/constants/wellknown/article/0,,1971,00.html>
| SOMMAIRE | Pages Web | Associations | Pages Personnelles | Algorithmes | Problèmes | Demos |
| Exemples | Java | Sujets | Papiers | Journaux | Cours | Tutoriels | Historiques |
| Biographies | Arts | Jeux | Archives | Liens |
| Exemples | Java | Sujets | Papiers | Journaux | Cours | Tutoriels | Historiques |
| Biographies | Arts | Jeux | Archives | Liens |
| Accueil | Plan du site | Bloc notes | Jeux | Graphes | Combinatoire | Arithmétique | Algèbre |
| Analyse | Probabilités | Automates | Informatique | Divers | Lycée |
| Analyse | Probabilités | Automates | Informatique | Divers | Lycée |
Advertising :
If you see a reference in one of the files that is not linked, and you know of a link address to the appropriate document,
please send me mail, and I will include the link in the document. Thanks very much in advance.
Avertissement : Le classement par catégories est approximatif. Certains liens se retrouvent dans des rubriques différentes et sur plusieurs pages. Les commentaires sont généralement des courts extraits des pages référencées. Il est possible que certains liens nécessitent une mise à jour.
Tous commentaires ou remarques sont les bienvenus, vous pouvez les adresser à :
Les mises à jour demandées sont réalisées dès que possible et, sauf si c'est nécessaire, aucun message de réponse n'est expédié. Merci de m'écrire.
Copyright © 1999-2012 Jean-Paul Davalan - Reproduction interdite.
Avertissement : Le classement par catégories est approximatif. Certains liens se retrouvent dans des rubriques différentes et sur plusieurs pages. Les commentaires sont généralement des courts extraits des pages référencées. Il est possible que certains liens nécessitent une mise à jour.
Tous commentaires ou remarques sont les bienvenus, vous pouvez les adresser à :
Les mises à jour demandées sont réalisées dès que possible et, sauf si c'est nécessaire, aucun message de réponse n'est expédié. Merci de m'écrire.
Copyright © 1999-2012 Jean-Paul Davalan - Reproduction interdite.