Spin III

Autres tours peu intuitifs présentés sur le site :
les trois portes et le tour de cartes du mathématicien William Fitch Cheney Jr. de l'université de Hartford.

Il serait faux de croire que le phénomène du spin n'existe qu'à « l'échelle microscopique ». L'expérience « macroscopique  » décrite ci-dessous, peut paraître déroutante au premier abord. On y observe le retour à l'état initial après une rotation de 2×2 π (deux tours), alors qu'une rotation de 2π (un seul tour) ne le permet pas.

L'expérience est décrite sur une autre page du site et est présentée ici comme un tour de prestidigitation.

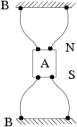
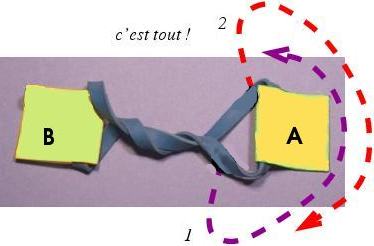
Dans le montage de R. Deheuvels (image de droite), le carton A est attaché par des ficelles aux deux parties fixes B. Dans l'expérience, on fait effectuer au carton deux tours complets autour de l'axe vertical NS et ensuite, sans plus faire bouger le carton central A, on dégage les ficelles afin de faire disparaître leur torsion pour revenir à l'état initial, sans passer au_delà des cartons fixes B.

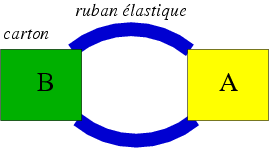Lorsque la ficelle est remplacée par un élastique plat et large on observe mieux les torsions et le système a une meilleure tenue.


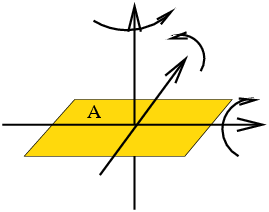
Chacun des cartons A et B est en double épaisseur.
Le large ruban élastique bleu, est inséré entre les deux épaisseurs collées de chaque carton.

Les trois manipulations décrites et photographiées correspondent à trois rotations d'un rectangle d'un angle de 4π selon les trois axes de la figure ci-contre. L'autre carton ne sert qu'à retenir l'élastique, vous pouvez le coller ou le fixer rigidement à un meuble ou à un mur et vous pourrez cependant effectuer toutes les manipulations à bases de rotations.

État initial





En effectuant un tour complet selon un axe horizontal AB, puis un deuxième tour dans le même sens au même carton, on obtient les positions suivantes :


     

Vous fixez solidement le carton B, pendant que vous tenez A d'une main et que de l'autre main, vous faites passer l'un des élastiques puis l'autre à la fois par-dessus A et par-dessous (ou l'inverse).




On pourrait semble t-il ne déplacer qu'un seul brin élastique, en contournant deux fois A. Mais cette manière de faire n'est pas acceptable car dans ce cas les deux brins élastiques sont vrillés. En utilisant des fils ou des ficelles on ne verrait pas cette déformation, d'où la nécessité de choisir des élastiques plats et larges.
C'est pour cette même raison qu'une rotation de 2 π de A ne peut être compensée par le déplacement des élastiques.

Important : tous les brins élastiques (un, deux ou éventuellement plus) peuvent être déplacés simultanément.

Il s'agit d'une rotation "à plat" de A. L'axe de rotation est perpendiculaire au plan de A. L'angle total de rotation est 2π.
Vous remarquez qu'une rotation de 2π et d'axe AB aurait le même effet sur l'élastique.

A tourne toujours de 2π dans une rotation de même axe et de même sens.
Alors que A passait la première fois au-dessus de l'élastique, on le fait passer maintenant au-dessous, ce qui permet à l'élastique de reprendre la position initiale.
(Si vous faisiez encore passer A du même côté de l'élastique, vous auriez une configuration semblable à celle du premier paragraphe de cette page et il vous faudrait ensuite dégager les élastiques).
On remarque encore qu'une rotation d'angle 4π permet de revenir à l'état initial, alors qu'une rotation d'angle 2π ne le permet pas.

Cette manipulation est tout à fait équivalente à celle-ci qui est bien connue :
1) Vous posez une assiette à plat sur votre main droite horizontale. 2) Vous faites tourner votre main, toujours à plat, dans le sens des aiguilles d'une montre; tout en levant d'abord le bras au-dessus de l'épaule (1/2 tour), puis en le redescendant (1/2 tour) pour arriver au niveau de départ. 3) Toujours en tournant le bras et en descendant, l'assiette arrive au niveau le plus bas (1/2 tour), ensuite faites remonter le bras jusqu'à arriver à la position initiale (1/2 tour), sans n'avoir jamais ni lâché ni retourné l'assiette et, ce qui est le plus important, avec le bras dans son état initial.

Remarque : évitez cette manipulation si vous avez la moindre contre-indication médicale, le bras effectue tout de même un tour sur lui-même (le deuxième tour compense le premier).

A glisse de droite à gauche en passant au-dessous de B



A revient à droite en glissant, mais cette fois il passe au-dessus de B.


Au paragraphe suivant, nous verrons comment revenir au point de départ par deux rotations, mais le plus intéressant est que cette fois encore, sans déplacer les deux cartons, il est possible de revenir à la position initiale, en jouant avec les deux parties de l'élastique. Mais je ne vous donnerai pas la solution, je vous laisse le plaisir de la découvrir par vous-mêmes.
Si vous ne trouvez pas la solution, vous pouvez effectuer les rotations décrites ci-dessous.

Les deux translations ci-dessus correspondent à une rotation d'angle 4 Π dont nous allons donner l'inverse, ce qui permettra de revenir à la position initiale, celle que l'on avait avant d'effectuer les translations.

Tout d'abord faisont subir à A une première rotation d'angle 2π d'ave vertical



La rotation précédente est suivie d'une deuxième rotation de 2π identique, de même axe vertical. Le système retrouve sa position initiale.

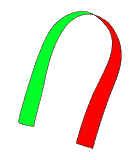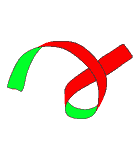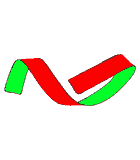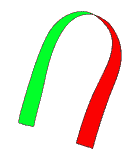
Deux tours ou rien Le ruban reprend sa position initiale après chaque période de deux tours.
La partie gauche du ruban est fixe, la partie droite effectue 2 tours complets dans le même sens en passant la première fois sous la partie gauche et la deuxième fois au-dessus.

L'image ci-dessous montre les deux tours d'une longue bande plane. Tirez sur les deux extrémités pour tendre la bande qui se mettra à plat. Cette fois les deux extrémités montrent la même face (de couleur verte) afin de permettre la mise à plat.

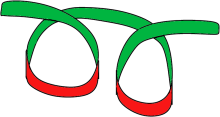
Deux tours
Si le ruban n'effectue qu'un tour, il ne se mettra pas à plat après étirement.

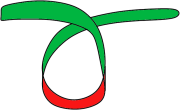
Un tour ne suffira pas


N'avez-vous jamais été surpris autrefois de certains comportements — aberrants et imprévus — de ces nappes qui reprenaient une 'bonne position' après avoir été tordues plusieurs fois dans le même sens ! (Ces nappes de fils ont disparu des boitiers d'ordinateurs récents).

Téléchargez la page A4 (Modèles adaptés à la découpe : pour droitier ou pour gaucher) et découpez la bande en forme de spirale correspondant à l'image ci-dessous.
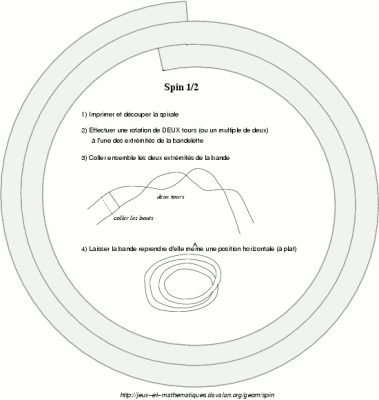
Découpez et collez.
(Attention, seul l'un des sens de rotation permet d'obtenir le résultat décrit).
Le mode d'emploi est détaillé sur la feuille.

1) Après avoir découpé aux ciseaux la bandelette, on fait effectuer deux tours complets à l'une des extrémités que l'on colle ensuite sur l'autre extrémité.
2) La bande reprend ensuite aisément une position "à plat', sans pliage.

Essayez la même manipulation en prenant une bande plane "classique" et comparez !

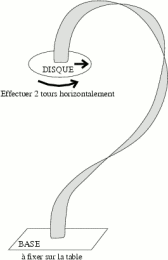Téléchargez la page A4 à découper et à coller pour construire le montage.

Sur la figure ci-après, l'une des extrémités de la bande est fixée à la table de travail (la base), l'autre extrémité est collée à un disque.
Faites tourner de disque de plusieurs tours selon un axe vertical. Gardez-le dans le même plan horizontal, pratiquement à la même place (et sans échanger les faces).
Observez les contorsions de la bandelette qui relie le disque à la table, (facilitez éventuellement le mouvement de cette bande). Tous les deux tours du disque, la bande et tout le système se retrouvent dans le même état.

Cette expérience et la propriété qu'à le disque de pouvoir tourner indéfiniment sont évoqués à l'aide d'un schéma à la page 85 du livre Motion Mountain - The Adventure of Physics (mais sans faire référence à la notion de spin ni à la périodicité).

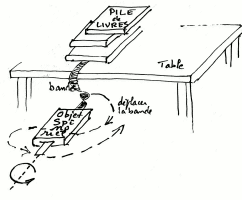À la page 205 de son livre "The Road of Reality" R. Penrose décrit une expérience sur un "spinorial object".
L'objet spinoriel est le livre que l'on fait tourner sur lui-même.
Une expérience semblable est suggérée sur l'image ci-contre.